СЛУЧАЙНЫЕ ОТКЛОНЕНИЯ

Вкусы у людей, как известно, чрезвычайно разные. Одни сникают при взгляде на длинные колонки цифр, на графики с ниспадающими и вздымающимися вверх ломаными и плавными кривыми, на масштабные стол­бики, высота которых описывает все, что угодно, — уро­жаи, рост, потребление водки или посещаемость теат­ров. У других же, и их немало, глаза загораются при ьзгляде па это богатство информации. Жадно рыщут они взглядом вдоль цифровых столбцов, просматрива­ют графики и приходят к интересным и важным вы­водам в области экономики страны, понимания чело — ловеческого характера или еще в чем-нибудь. Люди эти — статистики, — нужное и важное племя работ­ников, значительный отряд министерств и ведомств.

Задачи статистики (так называются не только люди, но и область деятельности) разнообразны и об­ширны. На десятках тысяч библиографических карто­чек приведены данные о промышленном производстве, о народном образовании, о смертности населения, о функционировании поликлиник и больниц, об авто­мобильных катастрофах, о посещаемости кинофильмов и бог весть еще о чем. Статистиков интересуют самые разные вещи: динамика роста тех или иных показате­лей, сопоставление данных по значению какого-либо параметра в разные времена года, или в разные часы дня, или среди мужчин и женщин, или среди лиц раз­ного возраста.

Особое место занимают в статистике измерения средних значений и отклонений от средних. Весьма распространены измерения роста и веса. Вес цыплят, которыми торгует птицеферма, интересен потому, что характеризует ее работу; рост людей интересен для швейной промышленности, выпускающей одежду от 46-го до 56-го размеров, и т. д. Так как все это изве­стно читателю из газет и радиопередач, приводящих всевозможные числа, то перейдем к нашей теме, а имен­но, к проявлению во всей этой массе чисел законов случая.

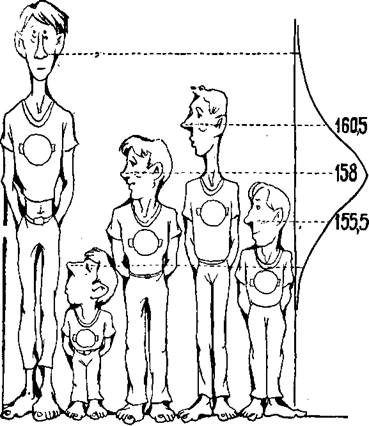
Один из скучных рисунков, фигурирующих в сочине­ниях по статистике, нам придется привести. Мы с художником долго ломали голову над тем, как сделать это масштабное построение более приемлемым в книге серии «Эврика». Результат творчества изображен на странице 71. Рисунок показывает диаграмму и кри­вую, которая носит название кривой статистического распределения.

Чтобы рисунок лучше рассмотреть, поверните, по­жалуйста, книжку на 90 градусов. Правда, новобранцы очутились в лежачем положении. Но, ей-богу, ничего более толкового не придумаешь. Теперь (в повернутом положении) высота кривой показывает число будущих

■олдат определенного роста. Величины роста нанесены іа уровне носа. Выбран конкретный пример измерения роста 1375 ребят. Столбики — это результат измере­ния, а плавная линия — наиболее близкая к опыту — гауссова кривая.

Статистикам известна следующая замечательная вещь: чем больше привлеченный для построения графи­ка материал (в данном случае чем больше ребят), тем плавнее и ближе к теории кривая, соединяющая верши­ны масштабных столбиков.

Самым замечательным обстоятельством является то, что кривая, получающаяся при измерении любых

)бъектов, имеет форму той же самой кривой Гаусса, на которую, как мы видели, ложатся числа комбинаций «красного» и «черного»!

Теперь рассмотрим вид кривой нормального рас­пределения в деталях. Нормальная кривая примерно похожа на колокол; она спадает одинаково в обе сто­роны сначала медленно, а потом быстро. Чтобы по­строить ее, математику достаточно знать три парамет­ра: высоту ее максимума, среднее значение изучаемой величины (то есть то место на горизонтальной оси, которое соответствует среднему значению) и ширину кривой. Вершине колокола как раз и соответствует то, что мы называем средней величиной. (Как получить среднее, известно даже тем, кто враждует с арифмети­кой: надо сложить все измерения и разделить на число измерений.) Откуда же видно, что максимум кривой Гаусса придется на среднюю величину? Доказатель­ство легкое: нужно проинтегрировать гауссову кривую. Но так как это занятие здесь неуместно, то просим поверить на слово, что теорема доказывается совсем просто.

Итак, остается пояснить, что такое ширина нормаль­ной кривой. Условно меряют ширину на полувысоте ко­локола. Очевидно, что ширина показывает, насколько часто или редко мы встречаемся с отклонениями от среднего. Чем уже колокол, тем реже значительные от­клонения от среднего.

Нормальная кривая распределения цоста, которая эыла нарисована на предыдущей странице, описывает­ся такими словами: «Высота кривой 200 человек»,

го есть двести человек имеют средний рост (первый, параметр кривой).

Заметим тут же, что иметь строго средний рост не­возможно, можно иметь средний рост с точностью 1, 2,

5 сантиметров и т. д. На нашем графике каждая точка представляет группу ребят, рост которых лежит в пре­делах 2,5 сантиметра. Средняя высота новобранцев, как мы видим по диаграмме, равна 158 сантиметрам — это второй параметр.

Третьим параметром является ширина колокола, равная в этом случае 15 сантиметрам. Знание ширины кривой позволяет сразу же оценить, с какими откло­нениями от среднего мы можем встретиться.

Нормальная кривая универсальна и относится

К любым событиям, поэтому, смотря все на тот же ри­сунок, мы можем делать общие заключения, справед­ливые для любых нормальных кривых. Скажем, откло­нения больше трех полуширин практически не встре­чаются. Так обстоит дело всегда, вне зависимости от того, о чем идет речь.

Для характеристики вероятности отклонения от среднего значения в технике и статистике существуют еще среднее отклонение по абсолютной величине, среднее квадратичное отклонение, вероятное отклоне­ние, мера точности. Все эти величины связаны между собой и с полушириной гауссовой кривой числовыми множителями, близкими к единице.

Вообще говоря, каких-либо доводов в пользу того, чтобы те или иные статистические сведения ложились на гауссову кривую нет. Правда, кое-что мы чуть позже увидим. Сейчас же надо подчеркнуть, что точные пред­ставления о нормальном распределении случайных со­бытий показывает кривая числа комбинаций «красного» и «черного». И к идеалу, с точки зрения математической, эта кривая приближается тем лучше, чем большее число испытаний проводится. Если число событий, кото­рые мы обрабатываем статистически, исчисляется де­сятками, то ординаты кривой будут отличаться от идеальных на десятые доли процента; при сотнях испы­таний разница уменьшится до сотых долей процента. Во всяком случае, на рисунке размером в страницу мы не отличим кривую распределения, построенную для тридцати событий, от гауссовой кривой идеальной.

Без преувеличения можно сказать, что закон Гаусса является важнейшим оружием в технике, в физике, в медицине — в любой науке.

Знание среднего значения случайной величины и ширины кривой нормального распределения позволяет уверенно судить о возможном и невозможном.

В технике беспорядочные колебания случайной ве­личины около ее среднего значения называют шумом. Такой шум вы слышите, когда снимаете телефонную трубку. Шумом называют обыкновенный белый свет. Шумит молния, излучая. весь спектр электромагнитных колебаний. Если шум изображать на телевизионном экране (осциллографе), то будет видна беспорядочная зигзагообразная кривая.

Шум нетрудно ограничить двумя горизонтальными линиями; так сказать, вписать его между нулем и не­которым максимумом. Что можно сказать об этом максимуме, о верхнем пределе шума?

В зависимости от природы, источника, от излуча­теля, шум может быть как угодно большим. По-одному шумит громкоговоритель в квартире, по-другому — на маленьком полустанке и совсем иной шум громкого­ворителей, работающих на улицах Москвы во время парада на Красной площади. Разница основательная. Но если построить графики этих трех шумов, то одну общую черту, продиктованную законом Гаусса, мы об­наружили бы без труда: верхний предел шума превы­шает средний шум примерно в четыре раза. То есть колокол гауссовой кривой весьма крутой и обрывается исключительно резко, несмотря на то, что с точки зре­ния формальной математики крылья кривой продолжа­ются в бесконечность. Из этого графика мы бы уви­дели, какое маловероятное событие становится прак­тически невозможным. Еще одно замечание: всякое заметное превышение шума над граничной горизон­талью, дающее более чем пятикратное отклонение от среднего шума, называется уже не шумом, а сигналом.

Кривая гауссова распределения показывает, на что надо, а на что не надо обращать внимания, когда речь идет о случайной величине. Физические измерения, как и математический анализ, показывают, что отклонения, не превышающие четырехкратного значения среднего от­клонения, являются нормой и поэтому не заслуживают ни особого внимания, ни объяснения. Скажем, извест­но, что физики могут измерять расстояния между ато­мами с точностью до 0,01 ангстрема. Некто Иванов публично заявил, что его измерения на 0,03 ангстрема отличаются от ранее полученных результатов, и пы­тается доказать, что его результат лучше имеющего­ся. Не стоило ему так поступать: не спорить ему надо, а сообщить ученому миру, что он лишь подтвердил ра­нее достигнутый физиками результат. Вот если бы его измерения отличались на 0,06 ангстрема, тогда другое дело; тогда можно было бы говорить, что какая-то из двух величин неверна и некто Петров был бы прав с точки зрения научной этики, приступив к измерению того же межатомного расстояния третий раз.

Зная гауссовы кривые для разных случайных собы­тий, статистики отвергнут газетное сообщение о ново­рожденном весом в 6 килограммов, о том, что в городе Киеве 12-го числа рождались только мальчики, а 13-го только девочки, о том, что в Москве в мае месяце не было ни одного дня с температурой ниже 30 градусов, о том, что число автомобильных катастроф в декабре было в десять раз больше, чем в январе, что во втор­ник по всему городу не было продано ни одного куска мыла, а в среду никто не приобрел в аптеке таблеток пирамидона и т. д.

И право же, такой скептицизм, базирующийся на хорошей статистике и знании закона вероятности, обо­снован не хуже, чем расчеты траектории космического корабля. Словом, невероятно — не факт.